Introduction à la Théorie des Jeux

La théorie des jeux est une branche des mathématiques qui s'intéresse à la prise de décision quand deux "joueurs" ou plus ont des intérêts en concurrence. Elle est souvent utilisée en économie ou en biologie et trouve aussi des applications dans le poker. La première partie de cet article présente les bases de la théorie des jeux qui nous permettront d'aborder son application au poker dans une seconde partie.
Photo: Russell Crowe dans Un Homme d'exception, film retraçant la vie de John Nash.
Le Dilemme du Prisonnier
L'exemple le plus connu de cette théorie est le dilemme du prisonnier. Beaucoup d'entre vous en ont sans doute déjà entendu parler, nous allons ici rentrer dans les détails.
Quelque part, un crime est commis et la police arrête deux suspects. La police est certaine que ces deux hommes sont impliqués dans le crime, mais n'ont aucune preuve. L'un des policiers a alors une idée. Il décide de mettre les prisonniers dans des cellules séparées et leur fait la proposition suivante:
Ils ont le choix entre dénoncer leur complice et passer moins de temps en prison ou ils peuvent tous deux garder le silence.
Si aucun des prisonniers ne parle, la police n'aura aucune preuve et les deux prisonniers iront en prison 1 an pour possession d'arme. Si l'un d'eux parle et l'autre garde le silence, le mouchard sera libre et l'autre ira en prison pour 10 ans. Si les deux prisonniers se dénoncent mutuellement, alors ils iront en prison pour 8 ans (et non 10 ans, car ils auront aidé la justice tous les deux).
Nous pouvons présenter ces informations sous forme de tableau :
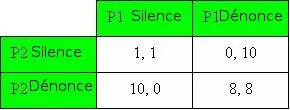
Ce tableau s'appelle une matrice où nous voyons tous les résultats possibles pour les deux "joueurs" (les prisonniers) impliqués dans ce jeu. Le premier nombre est toujours le résultat pour le premier prisonnier (P1) et le nombre après la virgule est le résultat pour le second prisonnier (P2). Si les deux prisonniers gardent le silence, ils iront en prison pour 1 an. Si l'un des prisonniers dénoncent son complice mais que l'autre garde le silence alors celui qui a parlé sera libre et l'autre ira en prison pour 10 ans. S'ils parlent tous les deux, tous deux iront en prison pour 8 ans. Le meilleur résultat possible pour la police est que les deux prisonniers se dénoncent mutuellement, rendant les rues plus sûres pour 8 ans. Et les policiers ont de la chance. Étant donné la proposition de départ, les deux prisonniers vont toujours se dénoncer tous les deux. Comment est-ce possible ?
Imaginons que nous soyons P1. Nous sommes assis dans notre cellule, réfléchissant à ce qu'il faut faire. Nous ignorons ce que fera P2 et nous n'avons aucun moyen de communiquer. Si P2 nous dénonce, alors il est préférable pour nous de le dénoncer également. Si P2, ne nous dénonce pas, alors notre meilleur choix est aussi de le dénoncer. Dans les deux cas, peu importe ce que choisit P2, le dénoncer vous permet de réduire le temps que vous passerez en prison.
Pour P2, la situation est exactement la même et il aura intérêt à nous dénoncer pour les mêmes raisons. Certes, P1 peut penser : "Peut-être que je ne devrais rien dire, si P2 fait de même, nous serons libres dans 1 an". Mais si P2 décide de parler, vous irez en prison pour 10 ans ! Avez-vous envie de prendre ce risque ? En général, non. Aussi, à la fin du "jeu", les deux prisonniers écoperont de 8 ans de prisons.
Cette situation s'appelle l'équilibre de Nash, d'après le nom du célèbre mathématicien John Forbes Nash. Vous pouvez en apprendre plus sur lui dans le film Un Homme d'exception (titre original: A Beautiful Mind). Lorsque cet équilibre est atteint, aucun joueur ne peut ajuster sa stratégie unilatéralement pour en tirer profit. C'est exactement ce qui se passe pour nos deux prisonniers. Imaginons que nous soyons sur le point d'équilibre de Nash, les deux prisonniers se dénoncent et vont en prison pour 8 ans. P1 peut changer sa stratégie et garder le silence, mais il ira en prison pour 10 ans et n'aura rien gagné. La situation est la même pour P2. Aucun changement unilatéral de stratégie ne peut profiter à ces "joueurs".
L'équilibre de Nash modifié par un nouveau joueur
Il existe des tas d'exemples possibles. Par exemple, supposons une guerre entre deux pays. Un pays peut choisir d'aller en guerre ou non. L'autre pays a le même choix. Si les deux pays renoncent à se faire la guerre, ils garderont tous deux leur territoire d'origine. Si le pays A fait la guerre mais que le pays B y renonce, alors A gagnera du territoire alors que B en perdra. Si B fait la guerre mais pas le pays A, c'est B qui agrandira son territoire au détriment de A. Si tous deux se combattent, alors tous deux subiront des pertes.
Nous pouvons présenter les différents résultats possibles sous forme de matrice. Si les deux pays conservent leur territoire d'origine, le score est de 0. Un territoire supplémentaire donne un score de 10 et un territoire perdu un score de -10. Si les deux pays subissent chacun des pertes, leur score est de -5.
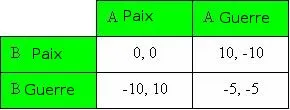
A nouveau, on constate que la meilleure option pour les deux pays est d'aller en guerre, quelque soit la décision de l'autre pays. Vous êtes le pays A. Si B attaque, vous pouvez décider de ne pas réagir (-10) ou de contre-attaquer (-5). La contre-attaque est ici la meilleure solution car elle réduit vos pertes. Si B ne vous attaque pas, vous pouvez choisir la paix (0) ou la guerre (10). A nouveau, la meilleure option pour A est d'aller en guerre, peu importe le choix de B. C'est pourquoi ces deux pays vont nécessairement entrer en guerre. C'est encore l'équilibre de Nash.
Nous pouvons alors imaginer que l'OTAN tente de garder le monde en paix et menace les deux pays : "Si vous entrez en guerre, nous vous bombarderons jusqu'à ce que vous retourniez à l'âge de pierre". Si l'OTAN décide de bombarder un pays, il subira des dommages encore plus grands. La matrice serait la suivante :
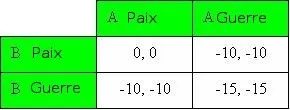
Maintenant, la situation est différente pour les deux pays. Si vous êtes le pays A, le pays B peut vous attaquer et vous aurez le choix entre la paix (-10) ou la guerre (-15). Maintenant, la paix est une meilleure option. Si le pays B choisit la paix, vous avez le choix entre la paix (0) ou la guerre (-10). Dans ce nouvel équilibre de Nash, la paix est le meilleur choix pour les deux pays. L'intervention de l'OTAN a modifié la matrice de façon à favoriser la paix.
La Théorie des jeux appliquée au Pair et Impair
Prenons à présent un exemple plus proche du poker. Le jeu s'appelle Pair ou Impair. Deux joueurs doivent prendre une décision au même moment. Ils disposent chacun d'une pièce et ils doivent décider de la garder ou non dans leur main. A un moment donné, les deux joueurs doivent ouvrir leur main et montrer s'ils ont gardé la pièce. Le nombre total de pièces visibles décide du gagnant. Si ce nombre est Pair (0 ou 2 pièces visibles), le joueur A gagne, si une seule pièce est visible (Impair), le joueur B gagne. Le joueur qui gagne reçoit le score de +1 point, celui qui perd, -1 point. La matrice des résultats sera:
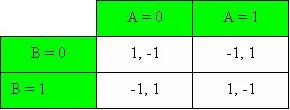
Ce jeu est ce que l'on appelle un jeu à somme constante. Parce que le total de la somme des différents résultats possible est toujours le même, en l'occurrence 0. Dans cet exemple, il évident que le joueur A essayera de toujours agir de la même façon que le joueur B, ainsi il y aura toujours 0 ou 2 pièces visibles et A sera gagnant. Le joueur B devra essayer de faire exactement le contraire du joueur A de telle sorte qu'une seule pièce soit visible.
Les deux joueurs peuvent s'observer et étudier le comportement de leur adversaire et réagir en conséquence. Dans ce cas, le plus observateur gagnera la partie. Mais il y a une autre option. Supposons que vous êtes le joueur B et vous pensez être moins bon observateur que le joueur A. Que pouvez-vous y faire ?
Imaginons que vous décidiez de montrer 0 pièce X% du temps et de montrer 1 pièce (1-X)% du temps. Le joueur A est meilleur observateur, il remarque notre comportement et choisit une option qu'il va appliquer 100% du temps. Admettons que vous décidiez de montrer 0 pièce 75% du temps et de montrer 1 pièce 25% du temps, alors X=0,75 et (1-X)=0,25. Le joueur A va vite s'adapter et choisir de de montrer 0 pièce 100% du temps afin de maximiser ses gains. Pourquoi ?
Nous pouvons calculer l'Expected Value (EV; c'est-à-dire l'espérance de gain sur le long terme) du joueur A :
EV(A) = (1)(X)(Y) + (1)(1-X)(1-Y) + (-1)(X)(1-Y) + (-1)(X-1)(Y)
où Y est le pourcentage de fois où A montre 0 pièce et X le pourcentage de fois où B montre 0 pièce. Cette formule peut sembler compliquée, mais ne vous laissez pas impressionner. A gagne 1 points s'il agit de la même façon que B et obtient -1 s'il agit de façon opposée. Puisque A est meilleur que B, il sait que X = 0,75 et 1-X = 0,25 et peut l'inclure dans son calcul d'EV.
EV(A) = (1)(0.75)(Y) + (1)(0.25)(1-Y) + (-1)(0.75)(1-Y) + (-1)(0.25)(Y)
EV(A) = 0.75Y + 0.25 – 0.25 Y – 0.75 + 0.75Y – 0.25Y
EV(A) = Y – 0.5
Tout ce que A à faire, c'est décider de la valeur d'Y. Nous savons que Y doit être compris entre 0 et 1 puisqu'il s'agit d'un pourcentage. Il devient évident que la valeur optimale pour A est Y=1. Son EV est alors égale à 1-0,5=0,5. Si A décide de jouer avec Y=1 et ne montre jamais aucune pièce, il gagnera 75% du temps pour un score de +1 et perdra 25% du temps pour un score de -1.
Ce qui nous donne : (0.75)(1) + (0.25)(-1) = 0.5.
Maintenant, imaginons que le joueur B fait exactement le contraire. Ainsi, X = 0,25 et 1-X = 0,75. Le calcul d'EV du joueur A sera :
EV(A) = (1)(0.25)(Y) + (1)(0.75)(1-Y) + (-1)(0.25)(1-Y) + (-1)(0.75)(Y)
EV(A) = 0.25Y + 0.75 – 0.75Y - 0.25 + 0.25Y -0.75Y
EV(A) = -Y + 0.5
Ceci est le calcul d'EV du joueur A après qu'il a découvert fréquence à laquelle B montre sa pièce. Nous voyons que le joueur A maximise son EV quand Y=0. Son EV est alors de 0,5.
Ce que fait A en tout premier lieu, c'est de découvrir quelle est la stratégie de B (car A est meilleur que B). Il évalue quel est le X de B, l'intègre dans son calcul d'EV et connait alors la valeur d'Y qui maximise son EV. Selon la stratégie choisie par B, A devra choisir la valeur d'Y qui sera toujours de 1 ou 0. Le joueur A va toujours choisir une action qu'il appliquera 100% du temps, car il sait que notre stratégie est la conséquence de sa meilleure observation.
Stratégie optimale contre la Nemesis
A cause de cet avantage, le Joueur A va toujours choisir la stratégie optimale contre B. A est la Nemesis de B. La Nemesis connait toujours notre stratégie et choisit toujours la meilleure contre-stratégie pour maximiser son EV. B s'en va dépité puisqu'il lui semble impossible de gagner.
Mais il revient un peu plus tard avec un nouvel espoir. Il cherche quelle est sa meilleure stratégie sachant que le joueur A va toujours réagir en appliquant la stratégie qui maximise son EV.
> Si le Joueur B décide de montrer 0 pièce plus de 50% du temps, son EV est :
EV(B) = (-1)(X) + (1)(1-X)
EV(B) = 1 – 2X
L'on s'attend à ce que le Joueur A retourne 0 pièce 100% du temps, parce qu'il est meilleur et connaît la stratégie de B. Si B montre 0 pièce X% du temps, A montrera aussi 0 pièce et aura un score de +1. Pour les (1-X)% du temps restant, B montre 1 pièce et A 0 pièce (à cause de sa stratégie optimale qui est de montrer 0 pièce 100% du temps) et B obtiendra +1 point.
> Si B décide de montrer sa pièce plus de 50% du temps, son EV est de :
EV(B) = (1)(X) + (-1)(1-X)
EV(B) = 2X – 1
L'on sait que le joueur A va montrer 1 pièce 100% du temps, toujours parce qu'il est meilleur que B. Si B montre 0 pièce X% du temps, la joueur A va montrer 1 pièce 100% du temps (sa stratégie optimale) et gagnera +1 point. Le reste du temps, (1-X)%, B montre 1 pièce tout comme A. Alors, A gagne +1 point et B obtient -1 point.
Dès lors, l'EV de B dépend de X. Souvenez-vous que X est égal au pourcentage de fois où B retourne 0 pièce. Nous avons maintenant deux calculs d'EV pour deux stratégies différentes. La stratégie 1 implique que B montre une pièce plus de 50% du temps, la formule est alors EV = 1 – 2X. La stratégie 2 suppose que B montre 1 pièce plus de 50% du temps, la formule est : EV = 2X – 1.
Si nous mettons ces deux formules sous formes de graphique, nous obtenons :
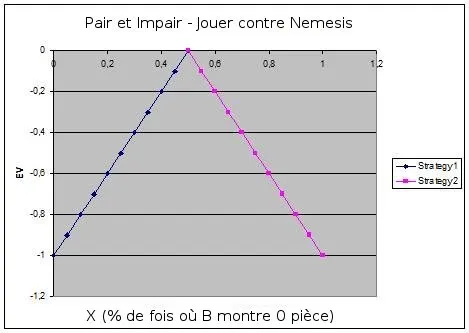
Nous pouvons conclure de ce graphique que pour le joueur B, la stratégie optimale est de montrer 1 pièce 50% du temps et de montrer 0 pièce les 50% du temps restants. Même si les résultats peuvent sembler évidents avec cet exemple simple, certaines situations sont bien plus complexes. Lorsque vous faites face à ces situations complexes, il est essentiel d'avoir compris le processus qui mène à ce résultat. La stratégie 1 est possible pour X compris en 0,5 et 1. La stratégie 2 est possible si X est compris entre 0 et 0,5. Les deux stratégies deviennent optimales quand X=0,5 et que l'EV=0.
Réalisant que pour toute autre valeur de X, l'EV de B est négative, il peut contrer la stratégie du joueur A en montrant sa pièce 50% du temps. Le joueur A n'a plus aucun avantage même s'il conserve son sens de l'observation ou qu'il connait à l'avance la stratégie de B. Quelque soit la stratégie choisit par A, il n'aura jamais une EV supérieure à 0. B est donc parvenu à neutraliser l'avantage du joueur A.
Cette méthode peut aussi être appliquée au poker, ce qui sera le sujet de la seconde partie de cet article.
10.000€ de freeroll chaque jour sur Bwin.fr
Bwin.fr propose 31 tournois freerolls quotidiens dotés de prize pool garantis allant de 150€ à 1.000€ pour une dotation journalière de 10.000€. Ouvrez votre compte aujourd'hui et bénéficiez d'un bonus de 500$ lors de votre premier dépôt.














